應用數學與交叉科學研究中心數學與纖維材料團隊在2023年10月19日上午10：00于崇真樓3028教室進行每周小組組會，小組全體成員和各位導師共同參加。在這次組會上，由一名研三和兩名研二的學生分别彙報自己的研究進展，然後老師與同學們對彙報内容進行學術探讨，并對存在的問題給出相應的指導和建議。

— 學生彙報内容展示 —

謝磊：本次組會介紹了受損樹狀分叉網絡中自發滲吸的分形模型。

自發滲吸因其在自然界的廣泛存在而引起了人們的廣泛關注。在本研究中，我們從理論上探讨了受損v形樹狀分支網絡的自發滲吸現象。此外，吸脹能力由兩個無因次量表征:吸脹勢和吸脹時間。然後使用分形理論生成這兩個無量綱量的解析表達式。在此基礎上，系統研究了結構參數對滲吸過程的影響。分支數N對吸脹勢有明顯的增強作用。引入了參數平面來可視化參數組合，從而能夠直接評估特定網絡系統中的吸脹過程。該模型揭示的物理機制為受損樹狀網絡的滲吸過程分析提供了有效的指導。

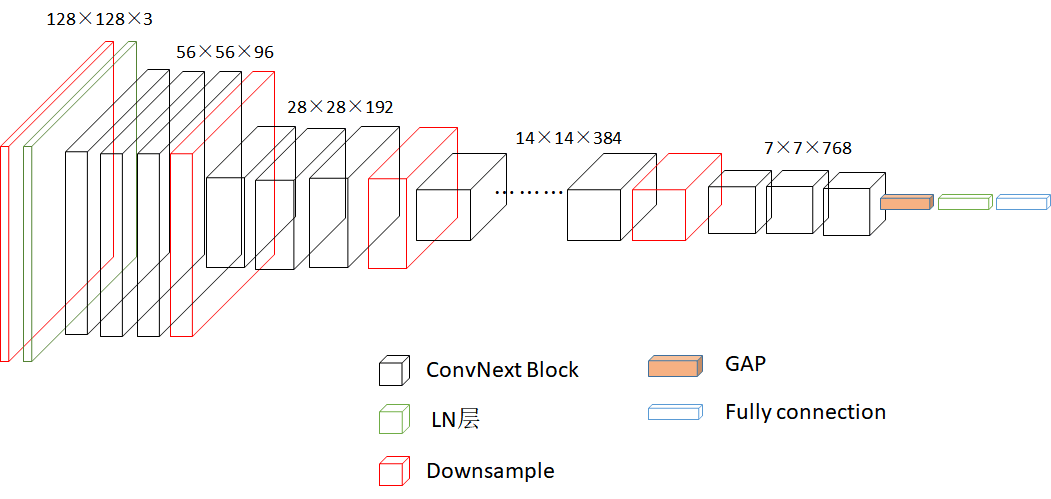
劉博：本次組會介紹了ConvNext的應用與改進。ConvNext是在卷積網絡領域足以媲美注意力機制模型的網絡，其主要結構由深度可分離卷積、GeLU激活函數、全連接層、LayerNorm歸一化層構成。在實際應用中，不同的數據集圖像特征不同，特别是在衛星圖像數據集中，因為其類間多樣性大、類内相似性大從而導緻模型提取特征困難，進而不得不考慮更改模型結構以适應不同的數據集。以BN替換LN，Relu替換GeLU，SSCOnv替換深度可分離卷積，讓模型提取的特征更傾向于衛星圖像數據是一種有效的手段。經過實驗，改進後的模型在精度上提升10.8%，但參數量略有增加。

楊淮：今日組會講述了關于分數階微積分猜想問題的證明思路，關于定理中的右側既對于分形連續函數的階黎曼-劉維爾積分圖像的上盒子維數是不超過函數圖像的盒子維數。文章中對于函數在定義區間上的變差做分割通過放縮以及積分中值定理得到了小分割上的上界，并且是對于任意的正階次的黎曼劉維爾積分算子都是滿足的。對于猜想的左側估計，楊淮同學借助豪斯多夫維度與盒子維數的關系對構造的豪斯多夫維數小于的情況進行讨論，對覆蓋進行放縮得到新的豪斯多夫測度，在保證豪斯多夫維度存在的情況下可以推導出關于分數階積分的階次是小于的。這就相當于證明了猜想的必要性。并且對與定理的充分性給出了兩種證明思路。